SPA-05
Interprocedural Analysis
¶Motivation
在常量传播中,y = addOne(42) 应该让 y 被视作一个常量(43),但是因为我们没有考虑过程间分析,就导致我们认为 y 是 NAC,这个结果过于保守了。
因此我们需要实装过程间分析。
¶Call Graph Construction (CHA based)
所谓 Call Graph,就是指出一个方法会在其方法体内,对哪些其它方法进行调用。
例如:
1 | T f(){ |
我们就能在 call graph 上构建一条边: T.f -> S.g。但是这个例子说着简单,现实中的情况是比较复杂的,这里我们就需要了解如何去构建 call gragh。
CG 的构造方法主要有以下几种:
- Class hierarchy analysis CHA
- Rapid type analysis RTA
- Variable type analysis VTA
- Pointer analysis k-CFA
越后面的越精确,而越靠前的速度越快,越有效率。
在 Java 中有多种 method call,其中 virtual call 对分析至关重要。
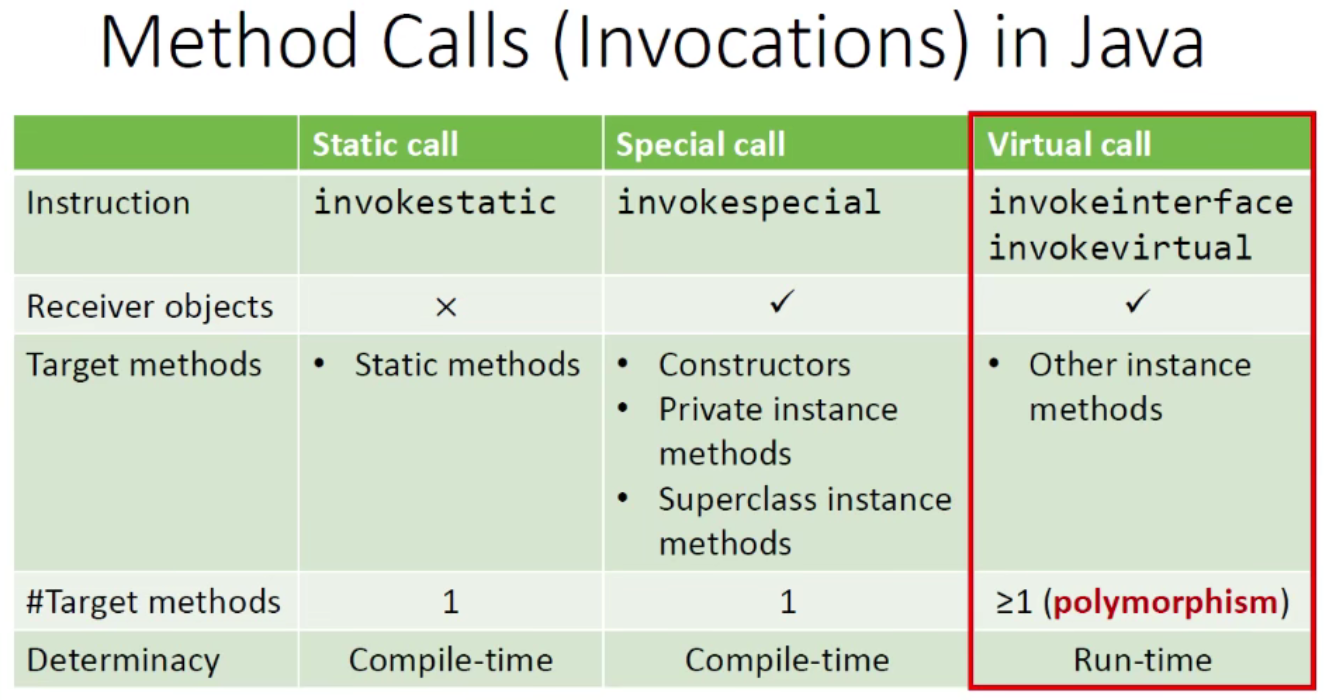
以下是简单介绍,看看就好。
- Instruction:指 Java 的 IR 中的指令
- Receiver objects:方法调用对应的实例对象(static 方法调用不需要对应实例)。
- Target methods:表达 IR 指令到被调用目标方法的映射关系
- Num of target methods:call 对应的可能被调用的目标方法的数量。Virtual call与动态绑定和多态实现有关,可以对应多个对象下的重写方法。所以 virtual call的可能对象可能超过 1 个。
- Determinacy:指什么时候能够确定这个 call 的对应方法。Virtual call 与多态有关,只能在运行时决定调用哪一个具体方法的实现。其他两种 call 都和多态机制不相关,编译时刻就可以确定。
在发生 virtual call 的时候,需要求解具体的方法究竟是什么。其中涉及到的机制叫 Method Dispatch.
具体来说,对于一条调用 y = x.foo(...);,在编译时我们不能立刻确定 x 所指向的是哪个对象(考虑 Number x = new One();,x 调用的就不是 Number 类的 foo 方法),而在运行时,我们会知道 x 会指向某个确切的对象 o,这个时候就可以去解析 o.foo(...) 的具体内容是什么了。
在 o.foo(...); 中,
- o 就是接收对象
- foo(…) 就是方法签名

给定对象的类 c 和函数签名 m,Dispatch 函数为:

这个方法就是在说,一个子类可能并没有自己实现某个方法,因此就要往父类去找,直到找到一个可用的实现位置。
例如,对于这样一个继承结构:
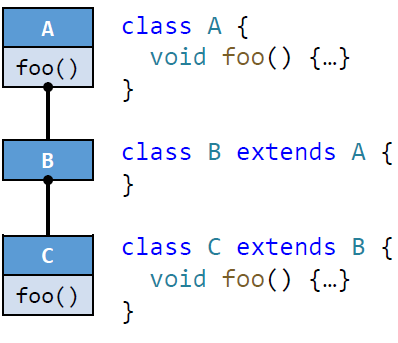
有着如下的 dispatch 结果:
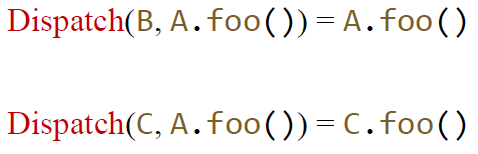
那么问题来了,刚刚说到,运行时是没法确定 y = x.foo(...) 的指向对象的。但是是不是完全没法确定呢?也不能这么说,1995 年,大牛 Jeff Dean 提出了一种方法:既然你也知道 Number x = ...,x 至少是 Number 类的对象。虽然我们不能知道 x 最后是 Number 对象还是它的一个子类对象,那么我们至少可以确定是 Number 及其继承类中的一个吧?
所以,我们这里就采用变量声明的类型来确定可能的 call 类型(即 Class Hierarchy Analysis, CHA)。下面就是解析一个方法调用对应的方法的算法:

第一种情况是 y = T.m(...),静态方法可以直接确定类是哪个,就不用去找继承结构了。
第二种情况是 new T(...),既然你知道你在调用谁的构造函数,那么也当然不用去找继承结构。当然还有其它的 special call(例如 this.m(...)),但是最后的结论都是一样的。
第三章情况就是 y = x.m(...) 了,这里的算法的意思是说,我把声明类型及其所有的子类都 dispatch 一遍,把可能的结果返回给你。
举个例子,现在有这么一个继承结构:
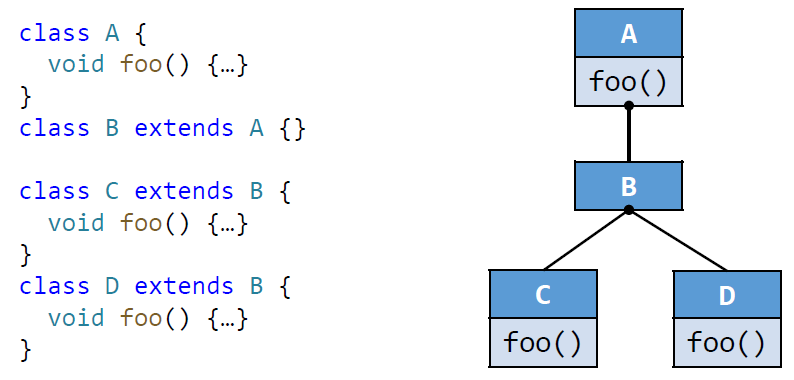
有着如下结果:
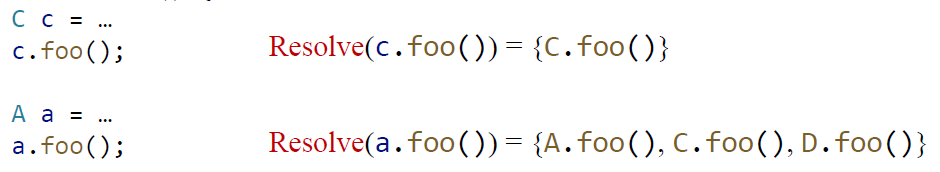
但是请考虑 B b = ...; b.foo()。按照算法,resolve 的结果是和 A 一样的,但是假设我们能知道,最后 B b = new B(),岂不是会多分析出两个可能的方法了?
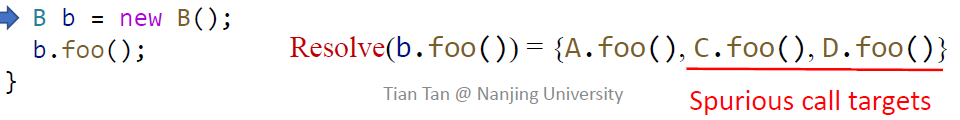
现在我们总结一下,基于 CHA 来构建 call graph 的优缺点:
- 优点:快,因为声明信息是很好获取的。
- 缺点:不够精确。这个问题需要指针分析来解决。
最后我们得到基于 CHA 来构建 call graph 的算法。

这个算法应该是很好理解的,它相当于是从 entry method 构建一个可达图。
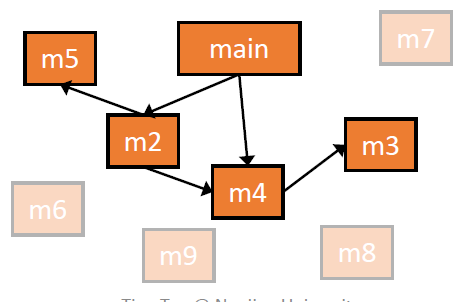
下面我们将展示讲义中例子的一个断点,来表述 CHA 的不精确性:
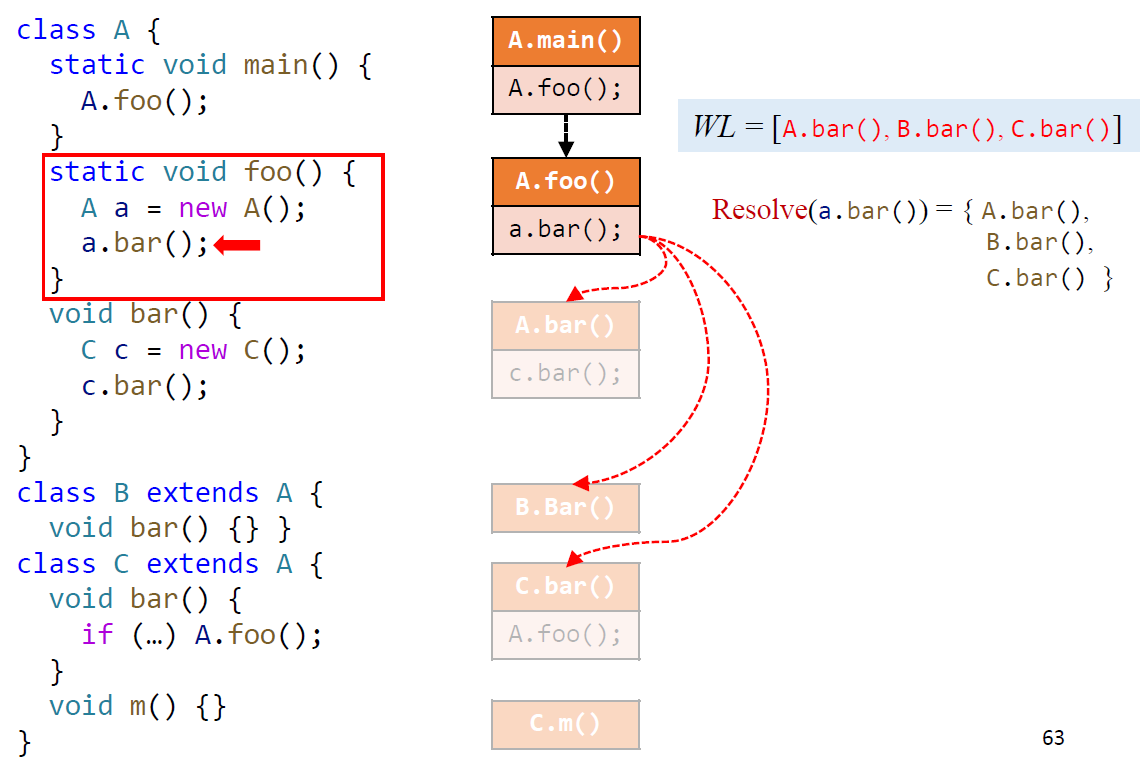
可以看到,A a 已经是明确指向 A 对象了,但是由于 CHA 的不精确性,我们依然往 B.bar() 和 C.bar() 加了边。
¶Interprocedural Control-Flow Graph
ICFG 就是通过在 CFG 的基础上加上 call edge 和 return edge。Call edge 是从 call site 连到 method entry 的,而 return edge 是从 method exit 连到 call site之后的一个语句的。(之所以是 exit 而不是 return 语句的 node,是因为可能存在多个 return 点,此时需要对这些 return 点做一个合并。)
那么我们要如何知道一个 call site 要往那个方法的 entry 和 exit 上连边呢?这就用到了刚刚说到的 call gragh 了。
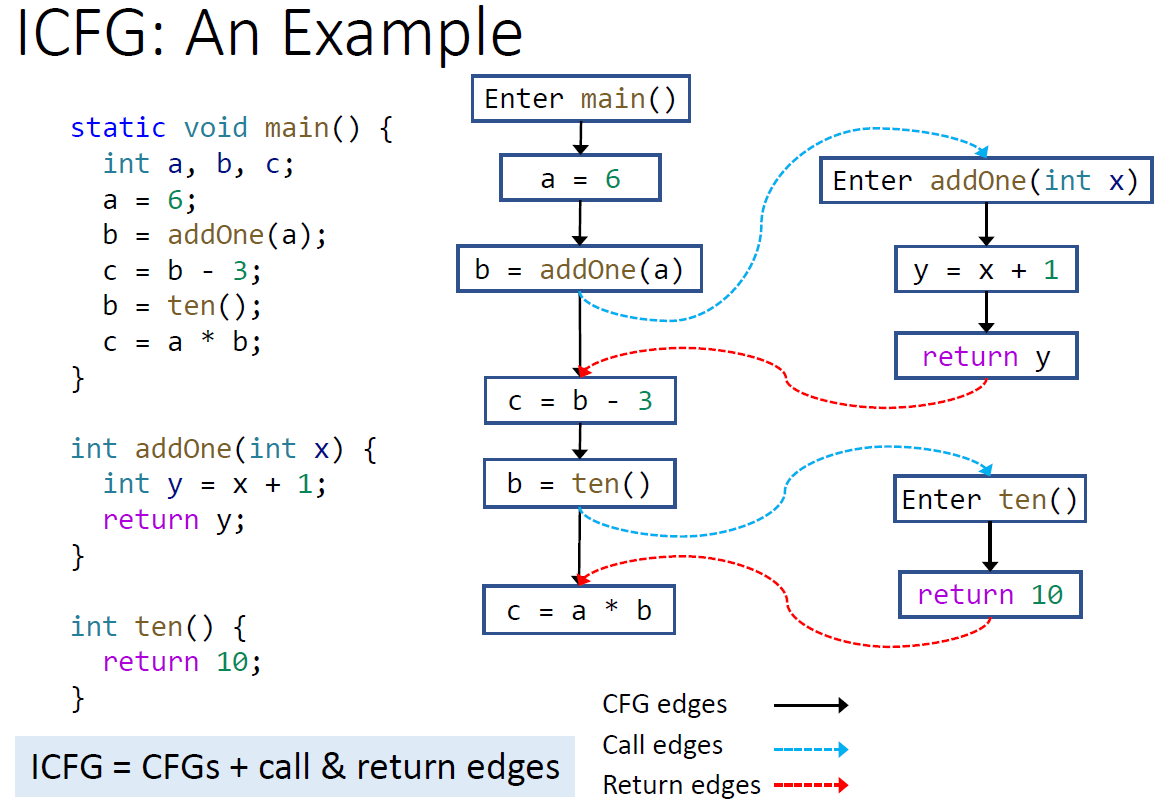
但是这样的修改还不够,因为会存在一些不精确性。具体请看下一章节。
¶Interprocedural Data-Flow Analysis
还记得过程内的数据流分析的两个要素:
- node 内如何使 data fact 发生变化;
- node 如何通过边收集/传递 data fact。
在过程内分析中,边只有一种,所以收集/传递时只需要原样传递 data fact。但是,考虑过程间分析后,我们就不能直接把 caller 的 fact 传到 callee 上了,而是应该通过方法的调用参数来进行 fact 的转换。
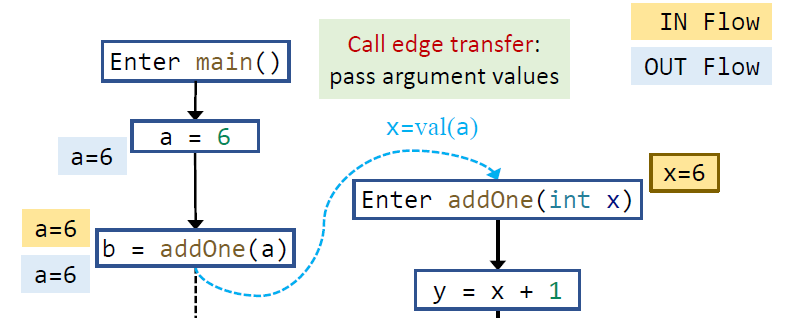
同样地,return edge 需要把返回值返回到接收变量上。
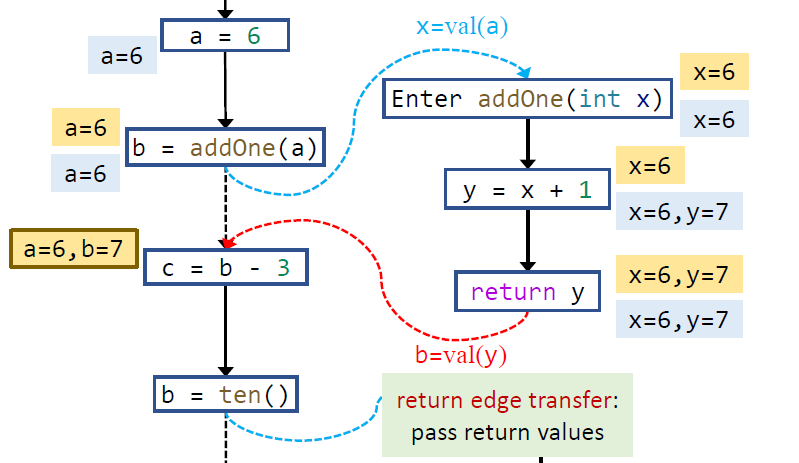
最后我们需要考虑一个问题:
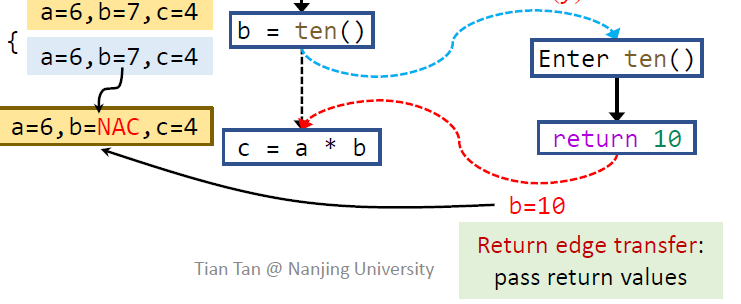
我们在过程间常量传播的设计中,caller 的 fact 会和 return value 冲突。一种自然的处理方法是在 call site 把 b 的值 kill 掉,2020 年的教学版本也是这么做的。但是,如果在 node 阶段就 kill 掉 b,那么如果 b 是方法调用的一个参数,就没有常量值可以传过去了。
因此,2021 年的版本明确了使用 call to return edge 来 kill 掉 b,遇到 call site 的时候,fact 直接原样复制。这就避免了上面所说的问题。
¶划重点
- 如何用 CHA 建 CG
- ICFG 的概念
- 过程间数据流分析的概念
- 过程间的常量分析

