排序算法

对各类排序方法整理如下：

排序算法 时间复杂度
归并排序 Ο(nlog2n)
快速排序 极端Ο(n2)，最好Ο(nlog2n)
堆排序 Ο(n)
计数排序 O(n+k),k为整数的范围
基数排序 Ο((n + k) d) ，n指分配n个数要n次，k指构建k个桶*，d为位数**)

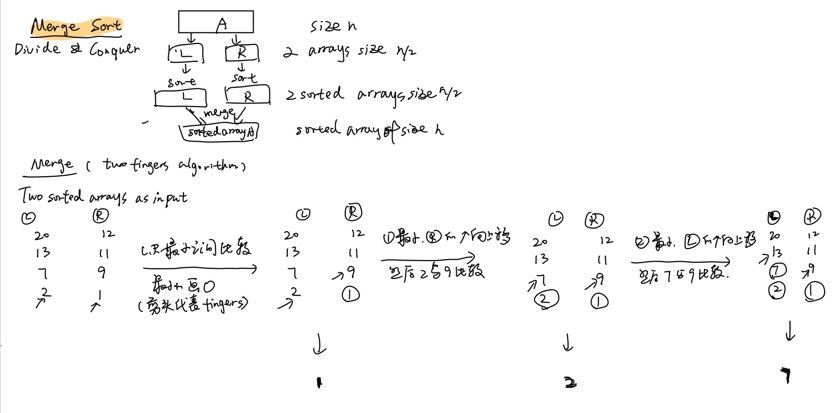
归并排序

如下图，假设要对长度为n的数列A进行排序，归并排序的思想就是Divide&Conquer分开并克服，首先将A着半拆分为左数列L和有数列R，然后分别对L和R进行各自的排序，最后进行L和R的合并操作。

img

在该课程里，讲师提到了归并排序用的是一种叫Two Fingers双指算法，这里我用上图的列子进行讲述：

  1. 如果数列a为[20,13,7,2,12,11,9,1]，将它折半拆为左数列L：[20,13,7,2]，右数列R：[12, 11, 9, 1];
  2. 对数列L和R各自进行排序，方法用冒泡排序或其他排序手段都行;
  3. 之后用箭头（指代手指）指向数列L和R最小的元素，进行比较，并先输出这个最小的元素，如上图就是min(1,2)=1。
  4. 之后在该最小元素下移动箭头至下一个元素，将其与原来另一个数列元素进行比较，如上图就是数列R的箭头移至9, 数列L由于上一步不是最小值，所以箭头不变，则对比箭头所指元素的到min(2, 9)=2，输出结果。重复上述操作箭头到达各自数列末尾。

如下图所示，这里复杂度为Ο(nlog2n)。这里可以简单的分为两块：（1）二路归并需要进行log2n次；（2）双指算法对单次二路归并进行n次箭头移动（帮助进行最小值比较操作）。因此就是nlog2n次。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
void Merge(int arr[],int low,int mid,int high){
    //low为第1有序区的第1个元素，i指向第1个元素, mid为第1有序区的最后1个元素
    int i=low,j=mid+1,k=0; //mid+1为第2有序区第1个元素，j指向第1个元素
    int *temp=new(nothrow) int[high-low+1]; //temp数组暂存合并的有序序列
    if(!temp){ //内存分配失败
        cout<<"error";
        return;
    }
    while(i<=mid&&j<=high){
        if(arr[i]<=arr[j]) //较小的先存入temp中
            temp[k++]=arr[i++];
        else
            temp[k++]=arr[j++];
    }
    while(i<=mid)//若比较完之后，第一个有序区仍有剩余，则直接复制到t数组中
        temp[k++]=arr[i++];
    while(j<=high)//同上
        temp[k++]=arr[j++];
    for(i=low,k=0;i<=high;i++,k++)//将排好序的存回arr中low到high这区间
		arr[i]=temp[k];
    delete []temp;//删除指针，由于指向的是数组，必须用delete []
}
 
//用递归应用二路归并函数实现排序——分治法
void MergeSort1(int arr[],int low,int high){
    if(low<high){
        int mid=(low+high)/2;
        MergeSort(arr,low,mid);
        MergeSort(arr,mid+1,high);
        Merge(arr,low,mid,high);
    }
}
//用非递归应用二路归并函数实现排序——分治法
void MergeSort2(int arr[],int n)//n代表数组中元素个数，即数组最大下标是n-1{
	/*
	int step = 1;
	while(step<n) //当元素个数不是2的幂时可能会出错，未考虑第2个序列个数不足的情况
	{
		for(int i=0;i<=n-step-1;i+=2*step)
			Merge(arr,i,i+step-1,i+2*step-1);
		step*=2;
	}*/
 
	int size=1,low,mid,high;
	while(size<=n-1){
		low=0;
		while(low+size<=n-1){
			mid=low+size-1;
			high=mid+size;
			if(high>n-1)//第二个序列个数不足size
				high=n-1;
			Merge(arr,low,mid,high);//调用归并子函数
			low=high+1;//下一次归并时第一关序列的下界
		}
		size*=2;//范围扩大一倍
	}
}

快速排序

它是一种非常高效也很常用的排序算法，主要有三个零件：left左指针，right右指针和base基准数。举个例子如下图所示：

img

  • 首先假设数列a为[6, 3, 7, 4, 1]，则left左指针为数列a最开始的元素6，right右指针为数列b最末端的元素1，base基准数为left左指针6（注意这个base基准数从头到尾都不改动的）。
  1. 先从right指向的数与base对比：
  • 如果right<base，则将right值替换left值，然后left向右移一位，同时right值替换为空值，且right指针位置不变，然后让left此时指的数与base对比。
  • 如果right>base，则将right值替换right值（即保持不变），然后right向左移一位，同时left值替换为空值，且left指针位置不变，然后让right此时指的数与base对比。
  1. 重复上述操作，直到左右指针重叠，此时就直接将base值放入重叠位置即可。

总结上面的就是：先右开始对比，之后’小于则替换left并移left，然后新left对比base’或’大于则替换right并移right，然后新right对比base‘, left和right重合后用base替换。它的时间复杂度取决于base值真实在排序后的位置，如果base刚好为排序中间的位置，时间复杂度为Ο(nlog2n)，如果base为数列最大值或最小值，则为Ο(n2)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//快速排序（从小到大）
void quickSort(int left, int right, vector<int>& arr)
{
	if(left >= right)
		return;
	int i, j, base, temp;
	i = left, j = right;
	base = arr[left];  //取最左边的数为基准数
	while (i < j)
	{
		while (arr[j] >= base && i < j)
			j--;
		while (arr[i] <= base && i < j)
			i++;
		if(i < j)
		{
			temp = arr[i];
			arr[i] = arr[j];
			arr[j] = temp;
		}
	}
	//基准数归位
	arr[left] = arr[i];
	arr[i] = base;
	quickSort(left, i - 1, arr);//递归左边
	quickSort(i + 1, right, arr);//递归右边
}

计数排序

计数排序并不基于元素的比较，而是一种利用数组下标来确定元素正确位置的算法。通过对每个数组中的每个元素进行相应的计数统计，通过计数值确定元素的正确位置的排序算法。计数排序需要知道待排序数据的取值范围，以方便申请辅助空间，这是计数排序的一个缺点。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void counting_sort(int data[], int n) {
  int* sorted = new int[n];
  int max = data[0];
  for (int i = 1; i < n; i++) {
    if (data[i] > max)
      max = data[i];
  }
  int* count = new int[max+1];
  for (int i = 0; i < max+1; ++i)
    count[i] = 0;
 
  // 记录频次
  for (int i = 0; i < n; i++)
    count[data[i]]++;
 
  // 累加计数
  for (int i = 1; i <= max; i++)
    count[i] += count[i - 1];
 
  // 确定最终位置
  for (int i = n - 1; i >= 0; i--) {
    sorted[count[data[i]] - 1] = data[i];
    count[data[i]]--;//注意
  }
 
  for (int i = 0; i < n; i++)
    data[i] = sorted[i];
 
  delete [] sorted;
  delete [] count;
}

基数排序

从低位开始，对所有数字进行排序。例如第1轮排序后，数字的个位数要有序；第2轮排序后，数字的十位数要有序，如果十位数相同的数，个位数要按照之前的相对顺序摆放；依次类推直至最高位排序完成。在对每位进行排序时，选择的排序算法一定要是稳定的排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
bool rxsort(int A[],int l,int h,int d,int k){
    if(NULL==A||l>h)
        return false;
    int size = h-l+1;
 
    int* counts = new int[k];//用于计数排序的辅助数据，详见计数排序
    int* temp = new int[size];//用于存储重新排序的数组
    int index;
    int pval=1;
    //依次处理不同的位
    for(int i=0;i<d;i++){
        //counts数组清零
        for(int j=0;j<k;j++)
            counts[j] = 0;
 
        for(int j=l;j<=h;j++){
            /*
            1.data[j]/pval：去掉数字data[j]的后i个数，例如：
            当data[j]=1234,i=2时，此时pval=100,data[j]/pval=12;
            2.(data[j]/pval)%k：取数字data[j]/pval的最后一位数
            3.(int)(data[j]/pval)%k:取数字data[j]的第i位数
            */
            index = (int)(A[j]/pval)%k;
            /*
            统计数组A中每个数字的第i位数中各个数字的频数,用于计数排序；
            */
            counts[index]++;
        }
        //计算累加频数，用户计数排序
        for(int j=1;j<k;j++)
            counts[j] = counts[j] + counts[j-1];
        //使用倒数第i+1位数对A进行排序
        for(int j=h;j>=l;j--){
            index = (int)(A[j]/pval)%k;
            temp[counts[index]-1] = A[j];
            counts[index]--;
        }
        //将按第i为数排序后的结果保存回数组A中
        for(int j=0;j<size;j++)
            A[j+l] = temp[j];
        //更新pval
        pval = pval*k;
    }
    delete[] counts;
    delete[] temp;
}